Badanie ma na celu wykazać przydatność programu GenMachine w rozwiązywaniu problemu optymalnej selekcji portfela. Ma również wykazać ścisłą korelację pomiędzy wartościami kryteriów prawdopodobieństwa (zysku) i ryzyka oraz portfeli wynikowych. Dane wejściowe zostały zaczerpnięte z przykładu przytoczonego w opracowaniu [5] Pawła Sewastianowa i Moniki Jończyk w celach porównawczych.
Zadanie zakłada, że inwestor dobiera optymalny portfel spośród pięciu znanych walorów. Oczekiwana stopa zwrotu każdego z walorów dana jest w postaci rozkładu Gaussa i przedstawiona na rysunku 4.24.
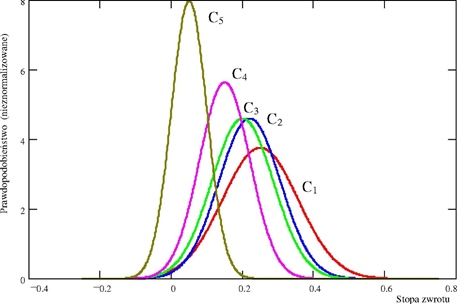
Rys. 4.24. Oczekiwana stopa zwrotu walorów C1, C2, C3, C4, C5 w postaci rozkładu Gaussa
Parametry charakterystyczne dla każdego z rozkładów podano w tabeli 4.1.
Tabela 4.1. Parametry charakterystyczne dla badanych rozkładów Gaussa
| Walor | Średnia arytmetyczna | Wariancja |
| Ci | 0,25 | 0,01125 |
| c2 | 0,22 | 0,00750 |
| c3 | 0,20 | 0,00750 |
| c4 | 0,15 | 0,00500 |
| c5 | 0,05 | 0,00250 |
Przejście od rozkładu Gaussa do liczby przedziałowej polega na odczycie wartości każdej funkcji reprezentującej stopę zwrotu, po znormalizowaniu do 1, w punktach przecięcia z wykresem funkcji g(x) = 0,01.
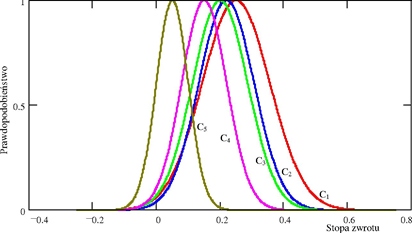
Rys. 4.24. Oczekiwana stopa zwrotu walorów C1, C2, C3, C4, C5 w postaci rozkładu Gaussa znormalizowanego do 1
Uzyskane wartości początku i końca każdego z przedziałów podano w tabeli 4.2.
| Walor | Początek przedziału | Koniec przedziału |
| Ci | -0,071 | 0,570 |
| c2 | -0,042 | 0,483 |
| c3 | -0,062 | 0,462 |
| c4 | -0,063 | 0,363 |
| c5 | -0,100 | 0,202 |
Tabela 4.2. Oczekiwana stopa zwrotu walorów C1, C2, C3, C4, C5 w postaci przedziałów
Optymalizowaną przez program GenMachine funkcją celu jest funkcja przedziałowa f (x) = x1 • Cj + gdzie xi..5 to zmienne sterujące, a C1..5 to stałe przedziały ostre. Populacja liczy 100 osobników, z których każdy reprezentowany jest przez wektor zmiennych sterujących w postaci liczb rzeczywistych [xi, x2, x3, x4, x5]. Operator selekcji turniejowej skonstruowany jest w ten sposób, że po obliczeniu wartości funkcji celu dla wszystkich genotypów bieżącej populacji, nadaje każdemu z nich rangę, dzięki zastosowaniu procedury sortowania szybkiego.
Procedura sortowania porównuje pary przedziałów poprzez obliczenie kryterium prawdopodobieństwa i kryterium ryzyka, a następnie zastosowanie agregacji addytywnej, tak jak zostało to opisane w podrozdziale 3.2 [cytowanej pracy magisterskiej].

