Ogólna koncepcja modelowania systemu eksploatacji została przedstawiona w rozdziałach poprzednich. W rozdziale tym rozbudowano tę koncepcję przede wszystkim na podstawie wniosków wynikających z rozważań dotyczących prakseologicznego ciągu systemów [14].
Typowy schemat sytuacji matematycznego modelowania decyzyjnego przedstawiono na rys. 5.4.
Zgodnie z przedstawionym na rys. 5.4. schematem, budując matematyczny model decyzyjny wybranego systemu należącego do ciągu prakseologicznego należy uprzednio:
- wybrać zasadę racjonalności, na podstawie której ustalimy kryterium modelu,
- określić intuicję potrzeb, dla których model jest budowany (umożliwi to nam określenie dziedziny modelu, jego relacji założeń oraz najbardziej istotnego problemu decyzyjnego).
- ustalić istotne parametry systemu oraz założenia metamodelowe (do założeń metamodelowych zaliczymy w szczególności te, zgodnie z którymi modelowany system traktujemy deterministycznie, stochastycznie lub growo).
Rys.5.4. Schemat sytuacji matematycznego modelowania decyzyjnego [14]
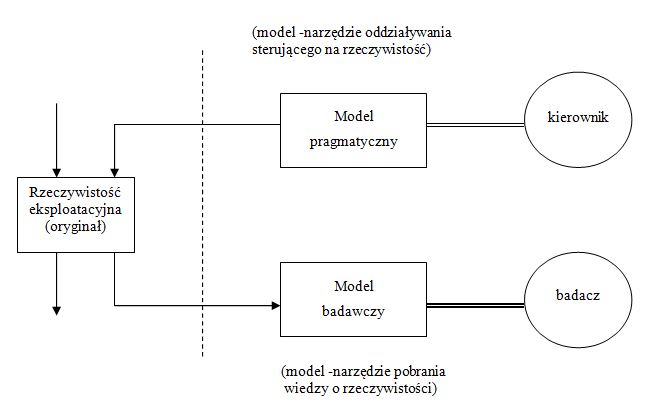
Koncepcję modelowania systemu przedstawioną na rys. 5.4. możemy zrealizować tylko wtedy, gdy poszczególne bloki tego schematu zostaną uprzednio wypełnione. Poniżej przedstawiona jest koncepcja wykorzystania do tego celu właściwości prakseologicznego ciągu systemów [14].
Niech będzie dany prakseologiczny ciąg systemów, którego fragment przedstawiono na rys. 5.5. Niech system Si, należący do tego ciągu, będzie tym systemem, dla którego mamy zbudować MMD. Bezpośrednie otoczenie systemowe systemu Si, niech stanowią systemy Si-1 oraz Si+1. Przyjmijmy, że z punktu widzenia modelowania systemu Si każdy z tych systemów charakteryzuje się zbiorem istotnych parametrów odpowiednio Xi, Xi-1 oraz Xi+1.
Rys. 5.5. Modelowany system oraz systemy ograniczające go

Koncepcję blokowego formułowania problemu decyzyjnego dotyczącego modelowania systemu Si można przyjąć w postaci następującej. Wyznaczyć takie X*i które spełni warunki:
1) Gi,i-1(Xi, Xi-1, Xi+1), miara jakości (kryterium);
2) Gi-1(Xi-1, Xi), ograniczenia potrzeb;
3) Hi+1(Xi+1, Xi), ograniczenia możliwości;
4) Mi(Xi, Xi-1, Xi+1) ograniczenia wewnętrzne.
Uwagi do przedstawionego schematu blokowego problemu decyzyjnego są następujące:
1) Miarę (wskaźnik) jakości albo kryterium podejmowania decyzji dla systemu modelowanego ustala się zawsze z punktu widzenia systemu zabezpieczanego przez system modelowany.
2) Zbiór rozwiązań definiują ograniczenia przyjęte w modelu. Mogą to być ograniczenia tylko trojakiego rodzaju: kumulowane ograniczenia od systemu poprzedzającego w ciągu system modelowany, kumulowane ograniczenia od systemu następującego w ciągu po systemie modelowanym oraz ograniczenia wewnętrzne systemu modelowanego.
3) Wyróżnione kryterium jakości podejmowanych decyzji (1) oraz ograniczenia (2), (3) i (4) są blokami problemu decyzyjnego.
4) Istotnym etapem modelowania decyzyjnego systemów eksploatacji powinno być blokowe formułowanie problemów decyzyjnych.
Z tego, co powyżej stwierdzono, można wyciągnąć praktyczne wnioski dotyczące poszukiwania zasad racjonalności, intuicji potrzeb oraz parametrów modelowanego systemu. Pozostaje jeszcze zaproponować koncepcję przyjmowania tzw. założeń metamodelowych. Założenia te dotyczą w praktyce zależności modelowanego systemu od czasu, od losu i od sytuacji decyzyjnej.
Przyjmując, że model systemu jest deterministyczny, zakładamy, iż wszyscy utajeni kierownicy tego systemu nie zakłócają rzeczywistego procesu kierowania.
Przyjmując, że wszyscy kierownicy systemu są zgodni, zakładamy, że nie działają oni w sytuacji growej.
Przyjmując, że właściwości modelowanego systemu nie zmieniają się z czasem oraz że kierowanie tym systemem nic zależy od czasu, zakładamy, iż wszystko dzieje się statycznie.
Tymczasem rzeczywisty system eksploatacji nie jest ani statyczny, ani deterministyczny, ani bezkonfliktowy. Dlatego też trzeba ze szczególną uwagą przyjmować wyróżnione tu założenia metamodelowe.
Dla przypadku, gdy problem decyzyjny dotyczy optymalizacji parametrów wybranego systemu kierowania, dokonuje się tzw. rozwinięcia prakseologicznego struktury kierowania tego systemu. Rozwinięcie to polega na tym, że dla systemu SK ustalamy jego bezpośrednie otoczenie systemowe składające się z systemu nadrzędnego SN i systemu roboczego SR. W każdym z tych systemów określamy zbiory istotnych parametrów wpływających na wartość wskaźnika jakości systemu optymalizowanego (rys. 5.6.) [14].
Rys. 5.6. Rozwinięcie prakseologiczne struktury systemu kierowania eksploatacją dla potrzeb matematycznego modelowania decyzyjnego [14]
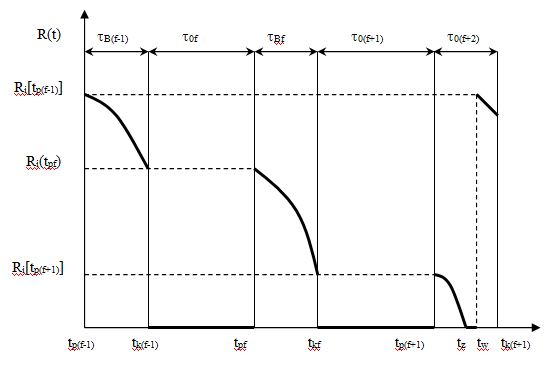
Blokowe sformułowanie problemu decyzyjnego w tym przypadku możemy przedstawić następująco:
Wyznaczyć takie X*SK, które spełni następujące warunki:
1) GSRD,SK(X*SK, YSRD, YSRI)= ekstr GSRD,SK (XSK, YSRD, YSRI);
2) GSRD(XSK, YSRD);
3) HSRI(XSK, YSRI);
4) MSK(XSK, ZSNI, ZSND).
Zauważmy, że warunek (1) definiuje X*SK za pomocą zbioru XSK a warunki (2), (3), (4) definiują zbiór XSK.

